Merge Sort

Merge Sort

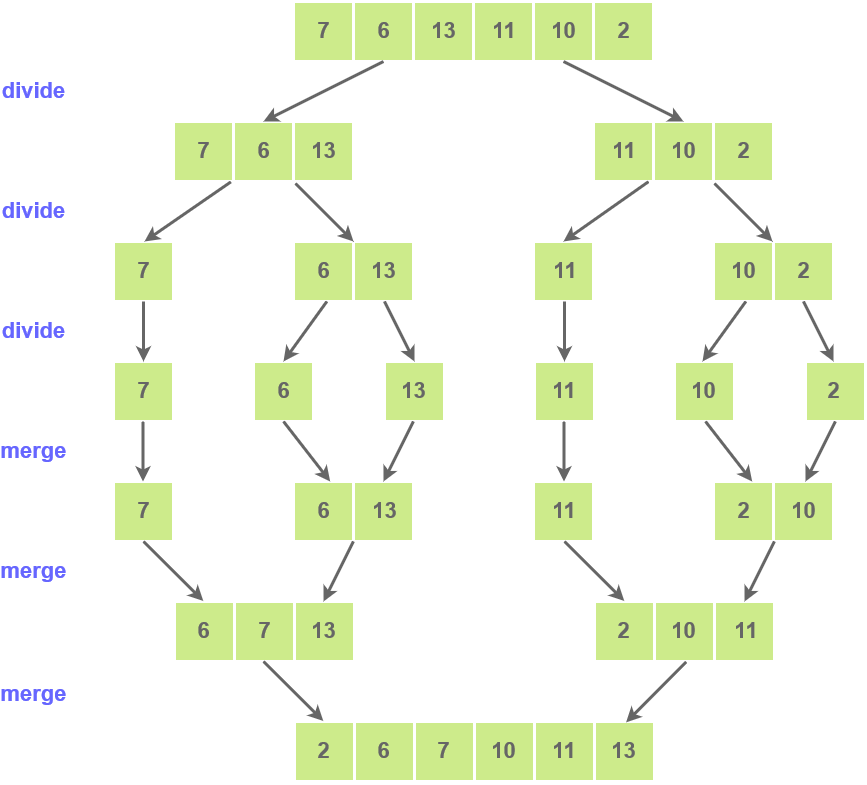
Merge sort is a sorting algorithm that works on the principle of Divide and Conquer. The array or list of elements is repeatedly broken down into several subarrays until each subarray consists of a single element. Then these subarrays are merged in a way such that the result is a sorted list.

Since the merge sort algorithm uses recursion to sort a given set of elements, it consumes less time.

Steps

1. Store the starting index of thearray in p and store the last index in r.
2. Store the middle index of array in q = (p + r)/2
3. Break the array into two subarrays, from p to q and from q + 1 to r index.
4. Divide these 2 subarrays again, just like the main array was divided.
5. Continue dividing into subarrays until subarrays of single elements get created.
6. Now start merging the arrays.

Code

void MergeSort(int A[], int p, int r)
{
    int q;
    if(p < r)
    {
        q = (p + r) / 2;
        MergeSort(A, p, q);
        MergeSort(A, q+1, r);
        merge(A, p, q, r);
    }
}

// function to merge the subarrays
void merge(int A[], int p, int q, int r)
{
    int B[5];   //sAme size of A[]
    int i, j, k;
    k = 0;
    i = p;
    j = q + 1;
    while(i <= q && j <= r)
    {
        if(A[i] < A[j])
        {
            B[k] = A[i];
            k++;
            i++;
        }
        else
        {
            B[k++] = A[j++];
        }
    }

    while(i <= q)
    {
        B[k++] = A[i++];
    }

    while(j <= r)
    {
        B[k++] = A[j++];
    }

    for(i=r; i >= p; i--)
    {
        A[i] = B[--k];  
    } 
}

Time Complexity : O(nlogn)