Quick Sort

Quicksort is a highly efficient sorting algorithm in which a list or array of elements is partitioned into smaller arrays.
A pivot(or central) element is selected in the array. The pivot element can be the first element, the last element, or any random element. The elements smaller than the pivot element are put to its left and greater elements to its right.

Implementation

Steps :

• Fix a pointer at the pivot element. Compare it with the elements starting with the first index. Set a second pointer for the greatest element.
• Set a third pointer to compare the pivot element with all the other elements. If an element smaller than the pivot element is found, swap the smaller element with the greater element.

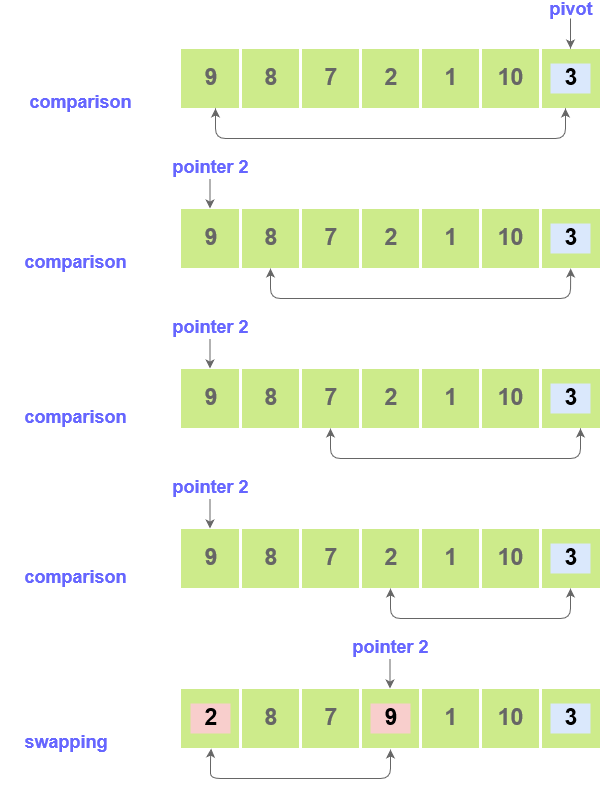
• This process is continued til the second last element is reached.
  The pivot element is then swapped with the second pointer.

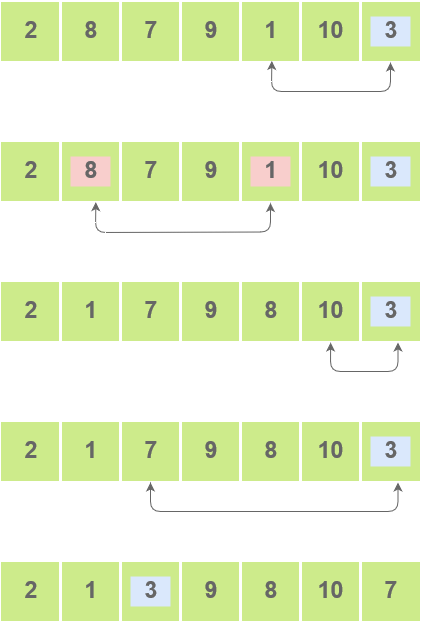
• Pivot elements are again chosen for each of the created sub arrays separately. These pivot elements are then placed at the their correct position. The elements smaller than the pivot element are then put on the left and the elements greater than the pivot element are put on the right.

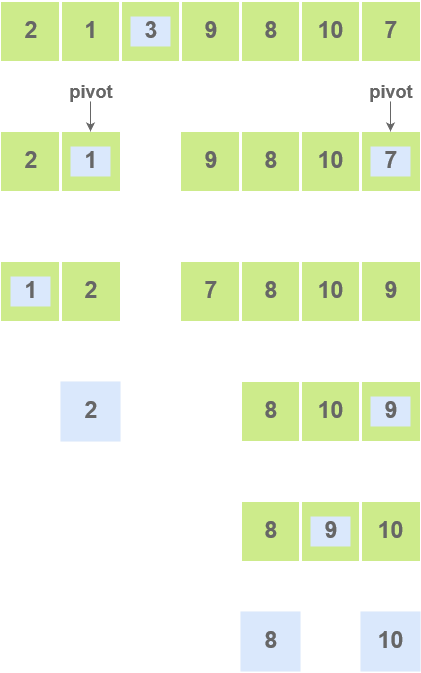
• The sub arrays are further divided into smaller subarrays until a single element sub array is created.
• The array is now sorted

Code:

// partition the A on the basis of pivot element
int partition(int A[], int start, int end) {

  int pivot = A[end];
  int i = (start - 1);

  for (int j = start; j < end; j++) {
    if (A[j] <= pivot) {
      i++;
      swap(&A[i], &A[j]);
    }
  }
  printA(A, 7);
  cout << "........\n";
  swap(&A[i + 1], &A[end]);
  return (i + 1);
}

void QuickSort(int A[], int start, int end) {
  if (start < end) {
    // Select pivot position and put all the elements smaller than pivot on left and greater than pivot on right
    int p = partition(A, start, end);

    // Sort the elements on the left of pivot
    QuickSort(A, start, p - 1);

    // Sort the elements on the right of pivot
    QuickSort(A, p + 1, end);
  }
}

Time Complexity : O(n^2)