Topological Sorting

In graph theory, a topological sorting of a directed graph is a linear ordering of vertices of graph such that if there is a directed edge uv from vertex u to vertex v, u comes before v in the ordering.

Note: Graph must be directed and acyclic.

Example Input

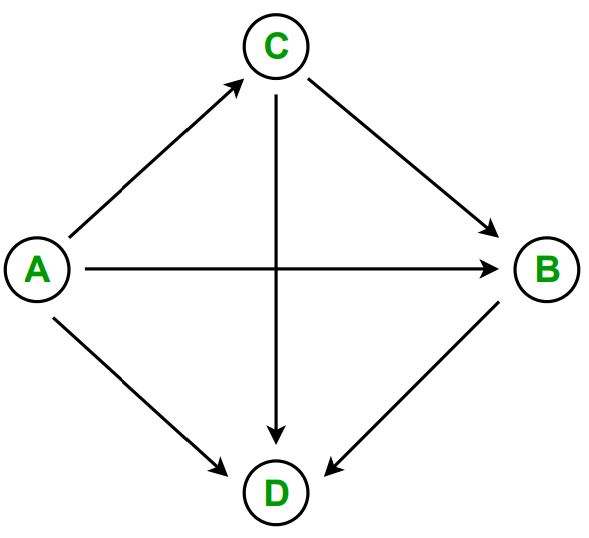
Expected Output

0 2 1 3

Pseudocode

solution(v,Check_Visited,sortGraph): 
    
    v <- visited

    for i in Graph[v]
        if i is not visited 
            // recursive call
            solution(i,Check_Visited,sortGraph) 

    insert v at first index of sortGraph

topologicalSort(): 
    sortGraph =[] 
    
    for i in range(V): 
        if i is not visited 
            // call
            solution(i,Check_Visited,sortGraph) 
    sortGraph <- print

Implementation in Python

from collections import defaultdict 
  
Graph = defaultdict(list) 
V = 0

def addEdge(u,v): 
    Graph[u].append(v) 
    
def solution(v,Check_Visited,sortGraph): 
    
    Check_Visited[v] = True

    for i in Graph[v]: 
        if Check_Visited[i] == False: 
            solution(i,Check_Visited,sortGraph) 

    sortGraph.insert(0,v) 

def topologicalSort(): 
    Check_Visited = [False]*V 
    sortGraph =[] 
    
    for i in range(V): 
        if Check_Visited[i] == False: 
            solution(i,Check_Visited,sortGraph) 
    print(*sortGraph)
  
V = 4
addEdge(0, 1); 
addEdge(0, 2); 
addEdge(0, 3); 
addEdge(1, 3); 
addEdge(2, 3); 
addEdge(2, 1); 
  
topologicalSort()