Complete Guide To Queue

Queue

Queue is a linear data structure, in which elements are inserted from one end called the rear, and the removal of existing elements takes place from the other end called front. Queue data structure utilizes both its ends, unlike the stack data structure.

Queue follows FIFO (First In First Out) principle, which means the first inserted element is removed first.

A real-life example of the queue data structure is a line of people standing in a bank, the person who entered first gets their work done first, and hence leaves first.

Insertion in the queue is done at the rear end, and the process is called Enqueue.
The process of removal of an element from the queue is called Dequeue, which is done from the front end.

ADT of Queue

Data

• space for storing elements
• front pointer for deletion
• rear pointer for insertion

front and rear are index pointers.

class Queue{
   int arr[50]
   int front, rear;
   int size;
};

Constructor to initialize size, front and rear :

  Queue(int n)
    {
    front = -1;
    rear  = -1;
    size =n; 
    }

Types of Queue

The following are the different types of queues :

1. Double Ended Queue
2. Circular Queue
3. Priority Queue

Operations on Queue

isFull

  bool isFull()
  {
    if (rear == SIZE - 1) 
      return true;
   return false;
  }

isEmpty

  bool isEmpty()
  {
    if (front == rear)
      return true
   return false;
  }

Enqueue

• First, check if queue whether queue is Full
• Initially, front = rear = -1.
• To insert element, move rear to next index, then insert element

note : First element is at index 0, but front remains at -1.

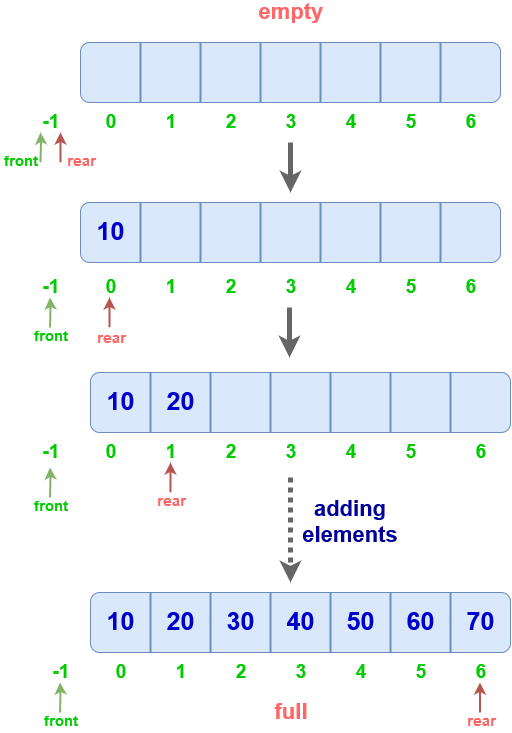
void enqueue(int x)
{
  if(rear==size-1)
     print("Queue Full"); 
  else  
   {      
     rear++;
     arr[rear]=x;    
   }
}

Time complexity : O(1)

Dequeue

• Check if queue is empty, if yes, print Empty Queue and return -1
• Move front to the next index and remove the element

note: front is kept before the 1st element and not on it.

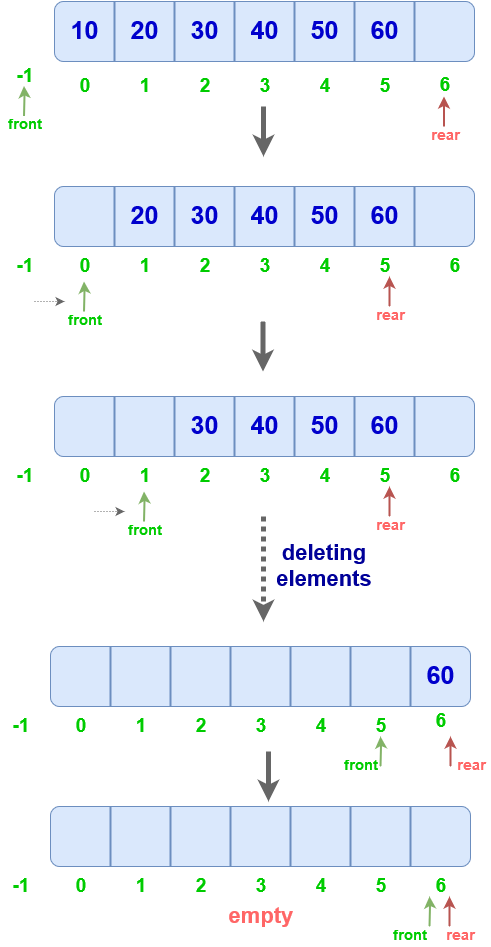
int dequeue()
{
    int x=-1;
    if(front==rear)
      print("Empty Queue"); 
    else
    {
      x=arr[front+1];
      front++;
    }
    return x;
}

Time complexity : O(1)

Display

Displaying a queue

void Queue :: display()
{
    int i;
    for( i = front; i <= rear; i++)
    {
        print(arr[i])
    }
}

Limitation of this implementation

After performing enqueuing and dequeuing several times, the size of the queue gets reduced. The indices 0,1,2,3 can not be used until after the queue’s indices are reset after removal of all the elements. This can be seen below :

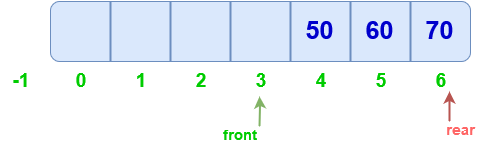
After the last element is removed, the front is at the rear and, the rear is at (size-1). This leads to the queue being both Full and Empty at the same time, which is wrong. The blank spaces cannot be utilized.

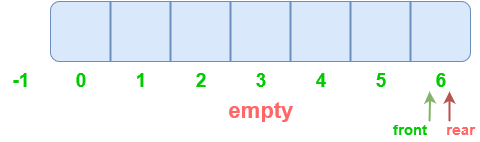
Solution:

1. Resetting the pointers: Setting front and rear to -1 after the queue is empty. But, this method does ensure the utilization of the free spaces as the queue has to be totally empty for resetting.
2. Circular queue: Using a modified queue to utilize the blank spaces.