Dequeue Data Structure

Double Ended Queue

Double Ended Queue is a type of queue data structure in which insertion and removal of elements can be performed from either from the front or rear. Unlike basic queue, it does not follow FIFO principle (First In First Out). It is also known as Dequeue.

Types of Dequeue

1. Input Restricted : Input is restricted to only one end but allows deletion at both the ends.

1. Output Restricted : Output is restricted to only one end but allows insertion at both the ends.

Operations on DEqueue

isFull

bool isFull()
{
    if((front == 0 && rear == size-1)||(front == rear + 1))
        return true;
    else
        return false;
}

isEmpty

bool isEmpty()
{
    if(front == -1)
        return true;
    else
        return false;
}

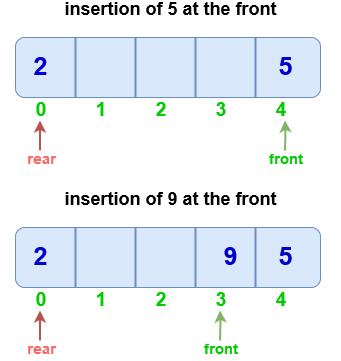
Insert at front

• Check if the queue is full (Overflow Condition)
• If the queue is empty then intialize front and rear to 0 (both point to the first element).
• Else, decrement front and insert the element.

Note : If front is equal to 0 then instead of decreasing it by 1, make it equal to size-1 (since circular array is used).

void push_front(int val)
{
    if(isFull())
    {
        print("OVERFLOW");
    }
    else
    {
        //If queue is empty
        if(front == -1)
            front = rear = 0;
          //If front points to the first position element 
        else if(front == 0)
            front = size-1;
        else
           front = front-1;        
  arr[front] = val;
    }
}

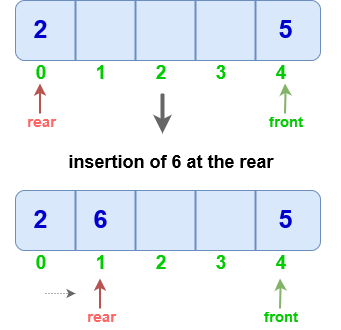
Insert at back

• Check if the queue is full (Overflow Condition).
• If empty, then intialize front and rear to 0 ( point both to the first element).
• Else, increment rear and insert the element.
  

  Note: If rear is equal to size-1 then instead of increasing it by 1 we make it equal to 0 (since circular array is used).

void pushBack(int val)
{
    if(isFull())
    {
        print(OVERFLOW);
    }
    else
    {
        //If queue is empty
           if(front == -1)
              front = rear = 0;

           //If rear points to the last element
        else if(rear == size-1)
            rear = 0;

        else
            ++rear;
    arr[rear] = val;
    }    
}

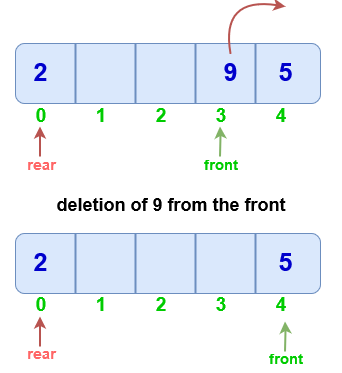
Delete from Front

• first check if the queue is empty. (Underflow)
• If only one element is present, make front and rear equal to -1.
• Else increment front.
  

  Note : If front is equal to size-1 then instead of increasing it by 1, make it equal to 0 (circular array).

void popFront()
{
    if(empty())
    {
        print(UNDERFLOW);
    }
    else
    {
        //If only one element is present
        if(front == rear)
            front = rear = -1;

        //If front points to the last element 
        else if(front == size-1)
            front = 0;

        else
            ++front;        
    }
}

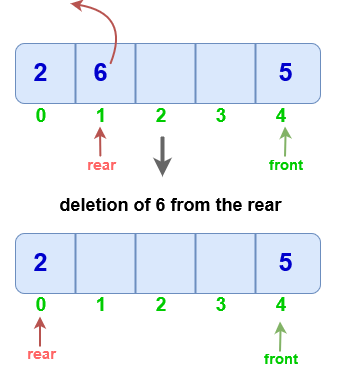
Delete from rear

• Check if the queue is empty.
• If only one element is present, make front and rear equal to -1.
• Else, decrement rear.
  

  Note :If rear is equal to 0 then instead of decreasing it by 1, make it equal to size-1.

void popBack()
{
    if(isEmpty())
    {
        print(UNDERFLOW);
    }
    else
    {
        //If only one element is present
        if(front == rear)
            front = rear = -1;

        //If rear points to the first position element 
        else if(rear == 0)
            rear = size-1;

        else
            --rear;        
    }
}

The time complexity of all the above operations is constant i.e. O(1).