Priority Queue Data Structure
Priority Queue
Priority Queues a type of queue data structure where an element is inserted from the back and removed from the front. The order of the elements in the priority queue depends on the priority of the elements.
Each element is associated with a priority in a priority queue. Elements with the same priority are served according to their order in the queue.
A basic queue data structure follows the First In First Out principle while in a priority queue, the elements are removed on the basis of priority. The element with the highest priority is dequeued first.

The structure of the element of the priority queue is:
class Node
{
int value
int priority
}
Priority Queue Operations
Basic operations of a priority queue are :
- Insertion
- Deletion
Priority queue is implemented using heap data structure. Therefore, it is important to be aware of the heapify operation :
void heapify(vector<int> &elem, int i)
{
int size = elem.size();
int largest = i;
int lc = 2 * i + 1; // left child
int rc = 2 * i + 2; // right child
if (lc < size && elem[lc] > elem[largest])
largest = lc;
if (rc < size && elem[rc] > elem[largest])
largest = rc;
if (largest != i)
{
swap(&elem[i], &elem[largest]);
heapify(elem, largest);
}
}
Enqueue
Inserting an element into a priority queue.
Steps for insertion into priority queue (max-heap) :
- create a new node if there is no node.
- Insert the new node at the bottom (last node from left to right.)
- heapify the array (convert the new tree into a heap.)
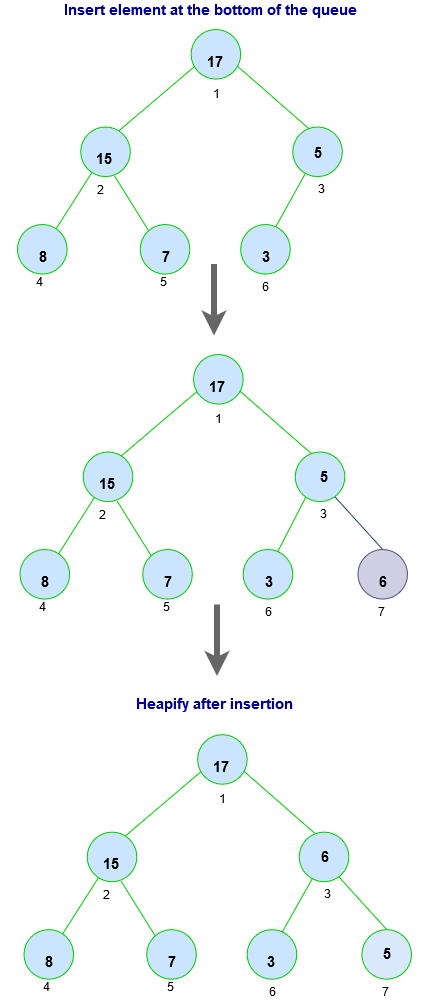
For Min Heap, modify it so that parentNode is always smaller than new node.
void enqueue(vector<int> &elem, int val)
{
int size = elem.size();
if (size == 0)
{
elem.push_back(val);
}
else
{
elem.push_back(val);
for (int i = size/2-1; i >= 0; i--)
{
heapify(elem,i);
}
}
}
Dequeue
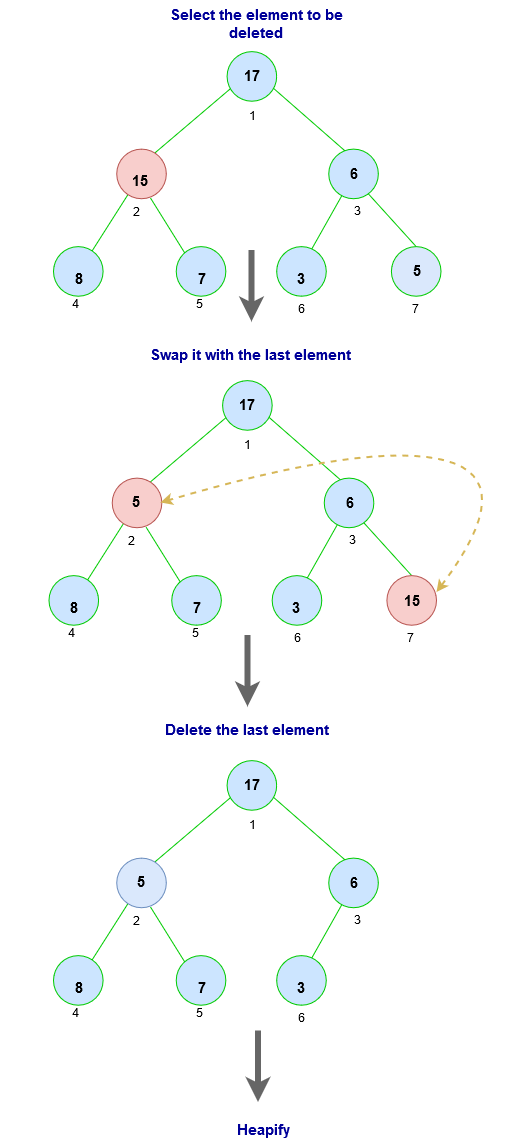
To delete element from a priority queue :
- Select the element to be deleted
- Swap it with the last element.
- Delete the last element.
- Heapify again
void dequeue(vector<int> &elem, int val)
{
int size = elem.size();
int i;
for (i = 0; i < size; i++) {
if (val == elem[i])
break;
}
swap(&elem[i], &elem[size - 1]);
elem.pop_back();
for (int i = size/2-1; i >= 0; i--)
{
heapify(elem,i);
}
}
Top or peek
// return top priority element
int top()
{
return arr[0]
}
Implementation of Priority Queue can also be performed using an array or a linked list. Among these data structures, implementation through heap is the most efficient.