Complete Guide To Trees

Tree Data Structure

A tree is a nonlinear data structure that is a collection of entities called nodes. Edges connect nodes. Each node contains a value, and it may or may not have a child node.

Unlike other linear data structures such as arrays, linked list, stack, and queue that store data sequentially, trees organize data hierarchically.

While performing any operation in a linear data structure, the time complexity increases with the increase in the data size.
Tree data structures allow better accessibility to the data as it is a non-linear data structure.

Tree Terminologies

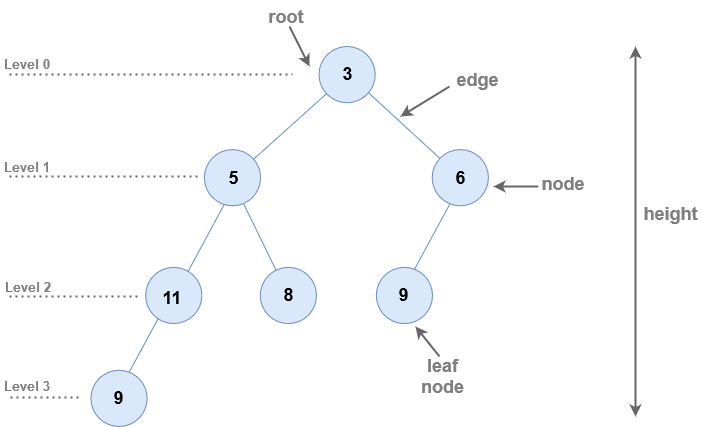
• Node : A node is an entity that contains a key or value and pointers to its child nodes.
  • Leaf nodes or external nodes : are the last nodes of each path that do not contain a link/pointer to child nodes.
  • Internal node : The node having at least a child node is called internal node.
• Edge : All tree nodes are connected by links called edges.
• Root : It is the first or topmost node of a tree.
  • Height of a Node : It is the length of the longest path to a leaf.
  • Depth (or Level) of a Node : It is the number of edges from the root to the node.
  • Height of a Tree : The height of a Tree is the height of the root node or the depth of the deepest node.
  • Degree of a Node : It is the total number of branches of that node.
  • Forest : A collection of disjoint trees is called a forest.

Types of Tree

1. Binary Tree
2. Binary Search Tree
3. AVL Tree
4. B-Tree

Tree Traversal

Traversing a tree is the process of visiting every node in the tree. Since all nodes are connected via edges, traversal is always started from the root node.
It is not possible to randomly access a node in a tree.

Basic structure of a tree

Every tree is a consists of :

• A node carrying data or a value
• Two subtrees

struct node 
{
    int data;
    struct node* left; // left child
    struct node* right; // right child
}

Note : The struct node pointed to by left and right might have other left and right children and should be considered as sub-trees instead of sub-nodes.

A hierarchical data structure like a tree can be traversed in three ways :

• In-order Traversal
• Pre-order Traversal
• Post-order Traversal

In-order Traversal

In inorder traversal, the output will produce sorted key values in ascending order.

Steps

Until all nodes are traversed :

• Traverse left subtree.
• Then the root node.
• Traverse right subtree.

Note : Every node may represent a subtree itself.

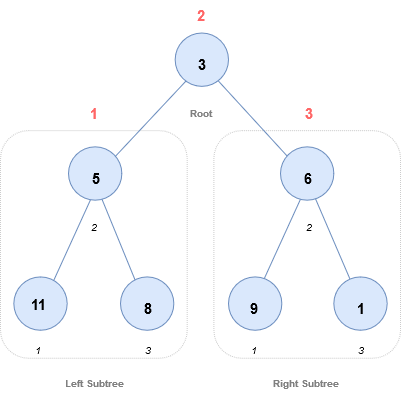
Start from 3, then move to its left subtree 5. 5 is also traversed in-order.
The process goes on until all the nodes are visited.
The output of inorder traversal of this tree will be :

11 → 5 → 8 → 3 → 9 → 6 → 1

Code

void inorder(struct Node* node) 
{
  if (node != NULL)
   {
    inorder(node->left);
    print(node->data);
    inorder(node->right);
    }
}

Preorder Traversal

Steps

• Visit root node.
• Traverse left subtree. (Visit all the nodes in the left subtree)
  • Traverse right subtree. (Visit all the nodes in the right subtree)

Note : Every node may represent a subtree itself.

Start from 3, then first visit 3 itself and then move to its left subtree 5. 5 is also traversed pre-order.
The process goes on until all the nodes are visited.
The output of pre-order traversal of this tree will be :

3→ 5 → 11 → 8 → 6 → 9 → 1

Code

void preorder(struct Node* node)
 {
  if (node != NULL)
  {
  print(node->data);
  preorder(node->left);
  preorder(node->right);
  }
}

Post-order Traversal

Steps

Until all nodes are traversed :

• Traverse left subtree.
• Traverse right subtree.
• Visit the root node.

Note : Every node may represent a subtree itself.

Start from 3,then traverse the left subtree 5. 5 is also traversed post-order.
The process goes on until all the nodes are visited.
The output of post-order traversal of this tree will be :

11 → 8 → 5 → 9 → 1 → 6 → 3

Code

void postorder(struct Node* node)
 {
  if (node != NULL)
   {
     postorder(node->left);
     postorder(node->right);
     print(node->data);
   }
}