Tree Traversals (In Order, Pre Order, Post Order)

Tree Traversal (In Order, Pre Order, Post Order)

Traversing a tree is the process of visiting every node in the tree. Since all nodes are connected via edges, traversal is always started from the root node.
It is not possible to randomly access a node in a tree.

Basic structure of a tree

Every tree consists of :

• A node carrying data or a value
• Two subtrees

struct node 
{
    int data;
    struct node* left; // left child
    struct node* right; // right child
}

Note : The struct node pointed to by left and right might have other left and right children and should be considered as sub-trees instead of sub-nodes.

A hierarchical data structure like a tree can be traversed in three ways :

• In-order Traversal
• Pre-order Traversal
• Post-order Traversal

In-order Traversal

In inorder traversal, the output will produce sorted key values in ascending order.

Steps

Until all nodes are traversed :

• Traverse left subtree.
• Then the root node.
• Traverse right subtree.

Note : Every node may represent a subtree itself.

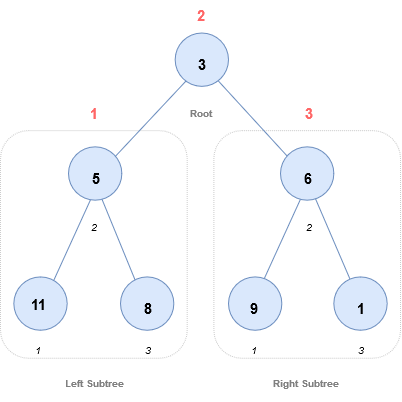
Start from 3, then move to its left subtree 5. 5 is also traversed in-order.
The process goes on until all the nodes are visited.
The output of inorder traversal of this tree will be :

11 → 5 → 8 → 3 → 9 → 6 → 1

Code

void inorder(struct Node* node) 
{
  if (node != NULL)
   {
    inorder(node->left);
    print(node->data);
    inorder(node->right);
    }
}

Preorder Traversal

Steps

• Visit root node.
• Traverse left subtree. (Visit all the nodes in the left subtree)
  • Traverse right subtree. (Visit all the nodes in the right subtree)

Note : Every node may represent a subtree itself.

Start from 3, then first visit 3 itself and then move to its left subtree 5. 5 is also traversed pre-order.
The process goes on until all the nodes are visited.
The output of pre-order traversal of this tree will be :

3→ 5 → 11 → 8 → 6 → 9 → 1

Code

void preorder(struct Node* node)
 {
  if (node != NULL)
  {
  print(node->data);
  preorder(node->left);
  preorder(node->right);
  }
}

Post-order Traversal

Steps

Until all nodes are traversed :

• Traverse left subtree.
• Traverse right subtree.
• Visit the root node.

Note : Every node may represent a subtree itself.

Start from 3,then traverse the left subtree 5. 5 is also traversed post-order.
The process goes on until all the nodes are visited.
The output of post-order traversal of this tree will be :

11 → 8 → 5 → 9 → 1 → 6 → 3

Code

void postorder(struct Node* node)
 {
  if (node != NULL)
   {
     postorder(node->left);
     postorder(node->right);
     print(node->data);
   }
}

Implementation

This implementation is based on concepts used in Array Implementation Of Binary Trees

#include <bits/stdc++.h>

using namespace std;

vector<int> tree = {-1, 3, 5, 6, 11, 8, 9, -1, 9, -1, -1, -1, -1, -1, -1, -1};

int leftChild(int i) {

return 2*i;

}

int rightChild(int i) {

return 2*i + 1;

}

int parent(int i) {

return i/2;

}

// Left, Root, Right

// Does in-order traversal for subtree located at index pos

void inOrderTraversal(int pos) {

if (pos < tree.size() && tree[pos] != -1) {

inOrderTraversal(leftChild(pos));

cout << tree[pos] << " ";

inOrderTraversal(rightChild(pos));

}

}

// Root, Left, Right

// Does pre-order traversal for subtree located at index pos

void preOrderTraversal(int pos) {

if (pos < tree.size() && tree[pos] != -1) {

cout << tree[pos] << " ";

preOrderTraversal(leftChild(pos));

preOrderTraversal(rightChild(pos));

}

}

// Left, Right, Root

// Does postOrder traversal for subtree located at index pos

void postOrderTraversal(int pos) {

if (pos < tree.size() && tree[pos] != -1) {

postOrderTraversal(leftChild(pos));

postOrderTraversal(rightChild(pos));

cout << tree[pos] << " ";

}

}

int main() {

cout << "In Order Traversal\n";

inOrderTraversal(1);

cout << "\nPre Order Traversal\n";

preOrderTraversal(1);

cout << "\nPost Order Traversal\n";

postOrderTraversal(1);

cout << "\n";

}